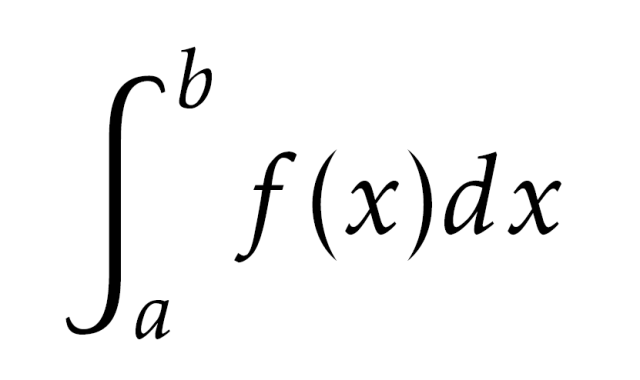Saya masih ingat waktu pertama kali belajar integral di bangku sekolah. Awalnya, saya pikir ini cuma soal rumus rumit yang mirip turunan tapi dibalik. Tapi makin saya pelajari, makin saya sadar: integ ral itu cara matematika menyatukan hal-hal kecil jadi sesuatu yang besar dan utuh. Seperti puzzle, tapi tiap potongan bisa tak hingga banyaknya.
Dan yang lebih menarik: ternyata integral itu bukan cuma soal angka. Ia hadir dalam dunia nyata—dari menghitung luas tanah, menghitung volume bensin dalam tangki mobil, sampai memperkirakan laba kumulatif perusahaan. Keren banget, kan?
Nah, dalam artikel ini, saya mau ajak kamu menyelami dunia integral dengan gaya santai, penuh contoh nyata, dan tetap informatif.
Apa Itu Integral dan Mengapa Penting?
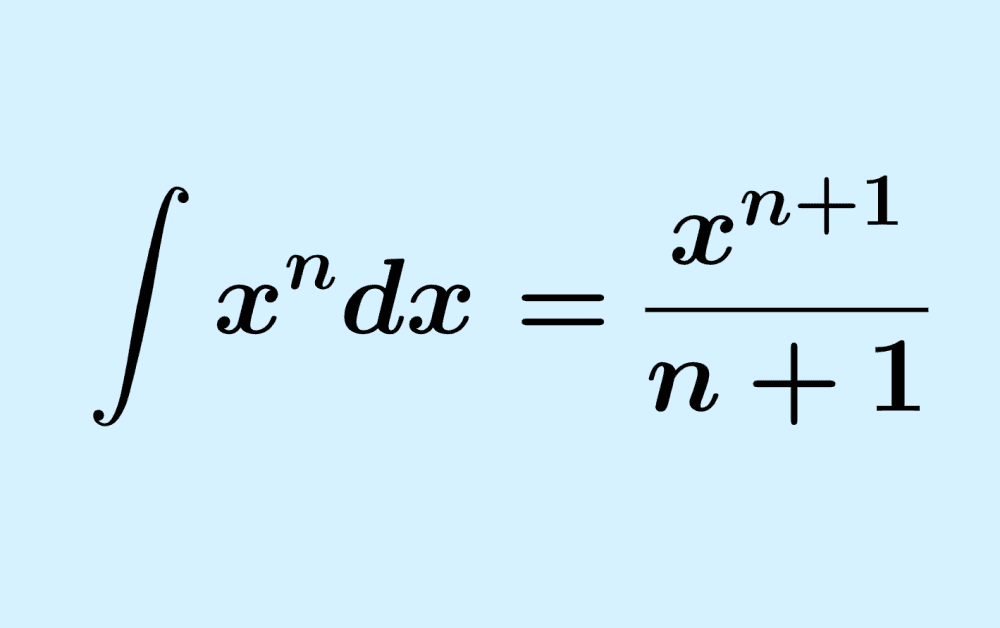
Integral, dalam pengertian paling dasar, adalah kebalikan dari turunan. Kalau turunan memecah sesuatu menjadi bagian kecil, integral menggabungkan bagian kecil jadi sesuatu yang utuh. Dalam bahasa kalkulus:
-
Integ ral tak tentu mengacu pada antiturunan fungsi.
-
Integ ral tentu mengukur luas, volume, atau total akumulasi dari sebuah fungsi di interval tertentu.
Contoh kasarnya: jika kamu tahu kecepatan kendaraan selama perjalanan, maka integral bisa bantu kamu cari jarak total yang ditempuh.
Dan nggak berhenti di situ. Integral juga jadi tulang punggung banyak bidang sains, teknik, bahkan ekonomi. Itulah kenapa kamu akan sering mendengar istilah ini di kuliah atau bahkan di dunia kerja.
Jenis-Jenis Integral: Tak Tentu dan Tentu
Integral Tak Tentu
Integral tak tentu biasanya ditulis sebagai:
∫ f(x) dx
Artinya adalah “cari fungsi F(x) yang jika diturunkan, hasilnya f(x).” Integral tak tentu tidak punya batas, dan hasilnya selalu mengandung konstanta C (karena saat kita menurunkan konstanta, hasilnya nol).
Contoh:
∫ 2x dx = x² + C
Integral Tentu
Integral tentu menghitung akumulasi dari f(x) dalam batas tertentu, biasanya ditulis:
∫[a to b] f(x) dx
Artinya, kita mau menghitung total area (atau nilai lainnya) dari titik a ke titik b di bawah kurva f(x). Pengetahuan ini yang sering dipakai untuk menghitung luas daerah, volume, atau jumlah total perubahan.
Contoh:
∫[0 to 2] x dx = [½x²]₀² = 2
Artinya, luas daerah di bawah kurva y = x dari 0 ke 2 adalah 2 satuan luas.
Aplikasi Integral dalam Kehidupan Sehari-Hari
1. Menghitung Luas dan Volume
Yang paling klasik dan sering diajarkan di sekolah. Misalnya kamu punya fungsi f(x) yang membentuk lengkungan, dan kamu mau tahu luas di bawah lengkungan itu, integral tentu jawabannya.
Volume? Sama. Misalnya kamu ingin tahu volume benda yang terbentuk dari perputaran kurva. Teknik ini dikenal sebagai integral dengan metode cakram atau kulit tabung.
2. Fisika dan Gerak
Dalam fisika, integral membantu kita menemukan:
-
Jarak tempuh dari kecepatan
-
Kecepatan dari percepatan
-
Gaya total dari distribusi gaya
Contoh: jika sebuah benda bergerak dengan kecepatan v(t), maka jarak totalnya dari t = a sampai t = b adalah:
∫[a to b] v(t) dt
3. Ekonomi dan Keuangan
Integral digunakan untuk menghitung:
-
Pendapatan kumulatif
-
Biaya total produksi
-
Persediaan rata-rata
-
Kurva distribusi pendapatan
Misalnya, dengan fungsi biaya marjinal C′(x), kamu bisa dapatkan total biaya C(x) dengan cara mengintegralkan.
4. Biologi dan Medis
Dalam dunia medis, integ ral digunakan untuk:
-
Menghitung kadar zat dalam darah sepanjang waktu
-
Model pertumbuhan populasi bakteri
-
Penghitungan luas area di bawah kurva dalam uji farmakokinetik
Pokoknya, integral ini diam-diam hadir di banyak proses sains dan kehidupan.
5. Ilmu Komputer dan Grafik Digital
Dalam dunia grafik dan pengolahan citra, integral berperan besar dalam:
-
Membentuk efek visual seperti blur dan pencahayaan
-
Mengukur perbedaan area warna
-
Simulasi fisika dalam game dan animasi
Meskipun kita jarang sadari, para pengembang software menggunakan integral dalam algoritma visualisasi yang kita nikmati setiap hari.
Integral dalam Dunia Pendidikan
Integral adalah bagian penting dalam kurikulum matematika tingkat SMA dan kuliah awal. Namun, banyak siswa yang kesulitan karena pendekatan yang terlalu rumit sejak awal.
Saya pribadi belajar integ ral dengan metode visualisasi. Melihat bagaimana luas di bawah kurva bisa dihitung dengan penjumlahan kotak kecil membantu saya paham konsepnya jauh lebih baik ketimbang menghafal rumus.
Sekarang banyak gu ru dan dosen pakai pendekatan grafis dan tools digital untuk bantu siswa. Salah satunya adalah Desmos, kalkulator grafik online yang sangat memudahkan pemahaman integral.
Integral dalam Bentuk Nyata: Contoh Skenario
Bayangkan kamu sedang mengisi bak mandi. Debit air (laju alir) berubah tiap menit, karena tekanan air menurun.
-
Fungsi debit: f(t) = 5 – 0.1t (liter per menit)
-
Kamu ingin tahu berapa liter air yang masuk selama 10 menit?
Caranya: integralkan f(t) dari 0 sampai 10
∫[0 to 10] (5 – 0.1t) dt
= [5t – 0.05t²]₀¹⁰
= (50 – 5) – 0 = 45 liter
Jadi, total air yang masuk ke bak adalah 45 liter. Praktis kan?
Perbandingan Integral dan Turunan
| Aspek | Turunan | Integral |
|---|---|---|
| Arah | Memecah jadi bagian kecil | Menggabung bagian jadi utuh |
| Simbol | f′(x), d/dx | ∫ f(x) dx |
| Fungsi utama | Laju perubahan | Luas, volume, jumlah total |
| Contoh | Kecepatan dari posisi | Jarak dari kecepatan |
| Hasil | Fungsi turunan | Antiturunan + konstanta (C) |
Dua konsep ini saling melengkapi dan menjadi inti dari kalkulus integ ral dan diferensial.
Tips Belajar Integral
-
Pahami dulu konsep luas
Jangan buru-buru ke rumus. Pahami dulu visualnya. -
Latih integral dasar berkali-kali
Semakin sering latihan, semakin mudah mengingat bentuk umumnya. -
Gunakan aplikasi pendukung
Seperti GeoGebra, Desmos, atau Wolfram Alpha untuk bantu simulasi. -
Pahami hukum integral
Seperti substitusi, parsial, dan properti garis batas. -
Buat catatan visual sendiri
Jangan cuma tulis angka—gambar kurva dan area yang dimaksud.
Integral Numerik: Kalau Fungsi Tidak Bisa Diintegralkan
Kadang kita ketemu fungsi yang tidak punya bentuk antiturunan sederhana, misalnya:
f(x) = e^(–x²)
Fungsi ini tidak bisa diintegralkan secara simbolik. Maka kita pakai metode numerik seperti:
-
Metode Trapesium
-
Metode Simpson
-
Monte Carlo Integration
Metode numerik ini banyak dipakai di komputer atau kalkulator untuk mendekati hasil integ ral.
Integral dan Teknologi Masa Kini
Dengan kemajuan AI dan machine learning, integral makin sering dipakai dalam:
-
Pengolahan sinyal
-
Neural network dan gradient descent
-
Algoritma optimasi
-
Pemrosesan citra medis
Bahkan software seperti MATLAB, Python (Scipy), dan R kini menyediakan library untuk pemodelan berbasis integral. Artinya, siapa pun yang ingin masuk dunia data dan sains harus paham minimal dasar integ ral.
Kesimpulan: Integral Itu Nyata, Bukan Sekadar Rumus
Buat saya pribadi, integral bukan cuma simbol ∫ dan rumus panjang. Ia adalah cara manusia memahami totalitas dari sesuatu yang kecil-kecil. Seperti menghitung luas hutan dari serpihan daun, atau menilai total penghasilan dari perubahan harian.
Kalau kamu selama ini menganggap integ ral itu sulit atau tidak relevan, mungkin kamu belum lihat aplikasi nyatanya. Coba perhatikan lebih dekat kehidupan sehari-hari—dari mobil yang kamu kendarai, tagihan listrik yang kamu terima, hingga grafik yang kamu lihat—semua punya unsur integ ral di dalamnya.
Jadi mulai sekarang, mari kita anggap integral bukan musuh, tapi alat. Karena dunia ini, pada dasarnya, adalah kumpulan bagian-bagian kecil yang ingin kita pahami secara utuh.
Tidak lagi tentang putri dan pangeran, sekarang juga ada: Buku Dongeng Modern: Cerita Klasik dengan Sentuhan Kekinian