Pecahan: Operasi Hitung, Perbandingan, dan Desimal

Waktu kecil, aku sempat benci banget sama pelajaran pecahan. Bukan karena gurunya galak, tapi karena rumusnya terlihat ribet—ada penjumlahan, pengurangan, perkalian, pembagian, penyebut yang harus disamakan, dan masih banyak lagi. Rasanya kayak diajak main puzzle tapi potongannya kecil-kecil dan gampang hilang.

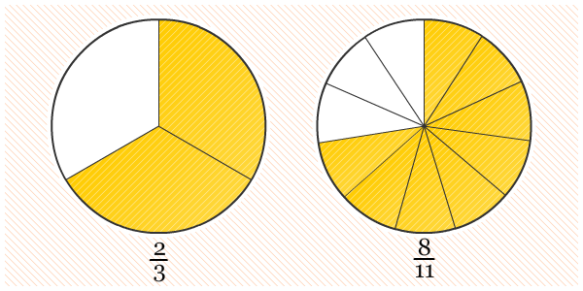
Tapi setelah aku ngerti konsep dasarnya, semuanya berubah. Pecahan itu justru logis dan dekat banget sama kehidupan kita. Bayangin aja, kamu mau makan pizza 1/2 atau 3/4? Kamu mau diskon 25% atau 1/5? Ternyata kita sering banget pakai tanpa sadar.

Jadi artikel ini aku tulis buat kamu yang pengen memahami pecahan dengan cara yang lebih ringan, lebih manusiawi, dan pastinya lebih membumi. Yuk mulai dari dasar dulu.

Apa Itu Pecahan?

Secara sederhana, pecahan adalah bagian dari keseluruhan. Dalam bentuk angka, ditulis sebagai:

ab\frac{a}{b}ba​

Di mana:

• a adalah pembilang (jumlah bagian)

• b adalah penyebut (total bagian)

Contoh: 14\frac{1}{4}41​ artinya satu dari empat bagian yang sama.

Aku pernah jelaskan pengetahuan ini ke keponakanku pakai donat. “Kalau donatnya dipotong jadi 4, dan kamu makan 1, itu artinya kamu makan 14\frac{1}{4}41​.” Langsung ngerti, karena dia suka makan donat. 😂

Jenis-Jenis Pecahan

Ada beberapa jenis pecahan yang perlu kamu kenali:

1. Pecah an Biasa: Bentuk umum, seperti 35\frac{3}{5}53​, 27\frac{2}{7}72​

2. Pecah an Campuran: Gabungan bilangan bulat dan pecahan, misalnya 1231\frac{2}{3}132​

3. Pecah an Desimal: Dinyatakan dalam bentuk desimal, misalnya 0,25 (setara 14\frac{1}{4}41​)

4. Pecah an Persen: Bentuk persentase, misalnya 75% = 34\frac{3}{4}43​

Mengetahui cara konversi antar bentuk ini sangat penting. Kita bahas lebih lanjut nanti.

Operasi Hitung Pecahan: Dasarnya Dulu

1. Penjumlahan dan Pengurangan

Hal paling tricky adalah menyamakan penyebut. Itu wajib biar bisa dijumlahkan/dikurangkan.

Contoh:

13+14\frac{1}{3} + \frac{1}{4}31​+41​

Samakan penyebut: 12

412+312=712\frac{4}{12} + \frac{3}{12} = \frac{7}{12}124​+123​=127​

Awalnya aku sering salah karena langsung jumlahin atas dan bawah: 1+13+4=27\frac{1+1}{3+4} = \frac{2}{7}3+41+1​=72​ — padahal SALAH BESAR. Ini kesalahan umum banget, bahkan orang dewasa kadang masih kejebak.

Untuk pengurangan, caranya sama. Misalnya:

34−16\frac{3}{4} – \frac{1}{6}43​−61​

Penyebut sama jadi 12:

912−212=712\frac{9}{12} – \frac{2}{12} = \frac{7}{12}129​−122​=127​

2. Perkalian

Justru lebih simpel. Langsung kali pembilang dan penyebut.

23×45=815\frac{2}{3} \times \frac{4}{5} = \frac{8}{15}32​×54​=158​

Enggak perlu samakan penyebut. Tapi kadang kamu bisa sederhanakan dulu sebelum dikali, supaya angka akhir lebih kecil.

3. Pembagian

Balik pecahan kedua (resiprokal), lalu kalikan.

23÷45=23×54=1012=56\frac{2}{3} \div \frac{4}{5} = \frac{2}{3} \times \frac{5}{4} = \frac{10}{12} = \frac{5}{6}32​÷54​=32​×45​=1210​=65​

Waktu aku ajarin anak tetangga, dia bingung kenapa harus dibalik. Jadi aku bilang: “Bayangin kamu punya 2/3 kue dan mau bagi rata ke 4/5 orang. Berarti kamu kasih 5/4 bagian dari 2/3 ke masing-masing.” Agak rumit, tapi begitu dia praktek langsung ngerti.

Menyederhanakan Pecahan: Supaya Lebih Ringkas

Kadang pecahan hasil hitung bisa jadi besar banget, misalnya 1824\frac{18}{24}2418​. Kita bisa sederhanakan dengan membagi pembilang dan penyebut dengan faktor yang sama:

1824=34\frac{18}{24} = \frac{3}{4}2418​=43​

Ini penting banget dalam soal-soal ujian, karena sering diminta jawab dalam bentuk paling sederhana.

Perbandingan Pecahan: Mana yang Lebih Besar?

Ada beberapa cara buat bandingin dua pecahan:

1. Samakan penyebut lalu bandingkan pembilang

2. Ubahlah ke desimal, misalnya 23≈0.666\frac{2}{3} \approx 0.66632​≈0.666 dan 35=0.6\frac{3}{5} = 0.653​=0.6, jadi 23\frac{2}{3}32​ lebih besar

3. Cross multiply (perkalian silang):

ab vs cd→a×d vs b×c\frac{a}{b} \text{ vs } \frac{c}{d} \rightarrow a \times d \text{ vs } b \times cba​ vs dc​→a×d vs b×c

Contoh:

23 vs 35\frac{2}{3} \text{ vs } \frac{3}{5}32​ vs 53​

$2\times 5=10$, $3\times 3=9$ → 23\frac{2}{3}32​ lebih besar

Aku sendiri paling sering pakai cara desimal karena lebih cepat dan pas banget kalau kerja pakai kalkulator.

Konversi Pecahan ke Desimal dan Persen

Pecahan ke Desimal

Tinggal bagi pembilang dengan penyebut.
Contoh:

34=3÷4=0.75\frac{3}{4} = 3 \div 4 = 0.7543​=3÷4=0.75

Beberapa pecahan punya desimal berulang, misalnya:

13=0.333…\frac{1}{3} = 0.333…31​=0.333…

Pecahan ke Persen

Tinggal kali 100:

34×100=75%\frac{3}{4} \times 100 = 75\%43​×100=75%

Sangat berguna dalam kehidupan sehari-hari: diskon toko, bunga bank, statistik, dll. Kalau kamu pengen belajar lebih dalam soal konversi pecahan dan desimal, Khan Academy punya penjelasan yang mudah diikuti dan interaktif banget.

Desimal ke Pecahan

Misalnya 0,8 = 810=45\frac{8}{10} = \frac{4}{5}108​=54​

Kalau 0,333…? Itu = 13\frac{1}{3}31​. Ada cara aljabar buat nentuin desimal berulang, tapi itu mungkin kita bahas lain waktu.

Pecah an Campuran dan Cara Mengubahnya

Kadang hasil hitungan pecahan lebih dari satu. Contoh:

74=134\frac{7}{4} = 1\frac{3}{4}47​=143​

Cara ubah pecahan biasa ke campuran:

1. Bagi pembilang dengan penyebut: 7 ÷ 4 = 1 sisa 3

2. Jadi hasilnya 1 34\frac{3}{4}43​

Sebaliknya, dari campuran ke biasa:

134=4×1+34=741\frac{3}{4} = \frac{4 \times 1 + 3}{4} = \frac{7}{4}143​=44×1+3​=47​

Aku suka pakai bentuk campuran waktu nulis jawaban soal cerita. Rasanya lebih “nyata” daripada pecahan biasa.

Pecah an Dalam Kehidupan Sehari-Hari

Kamu mungkin nggak sadar, tapi pecahan itu ada di mana-mana:

• Memasak: 1/2 sendok teh, 3/4 cangkir

• Diskon: 25% = 1/4

• Waktu: 15 menit = 1/4 jam

• Peta atau denah: skala 1:100 berarti 1/100 ukuran asli

Waktu aku belajar bikin kue, resep bilang “1/3 cangkir minyak”. Awalnya bingung, tapi akhirnya belajar cara ukur pecahan dan jadi makin paham pentingnya akurasi.

Kesalahan Umum yang Harus Dihindari

1. Jumlahkan langsung atas dan bawah → salah banget

2. Lupa samakan penyebut sebelum tambah/kurang

3. Salah balik pecahan waktu membagi

4. Nggak menyederhanakan hasil akhir

Aku sendiri pernah dihukum remidi karena asal nambahin pecahan tanpa nyamain penyebut. Tapi dari situ aku belajar: pecahan itu bukan sekadar hitung-hitungan, tapi latihan berpikir terstruktur.

Tips Belajar Pecahan Biar Nggak Stres

• Visualisasi pakai benda nyata (roti, kue, potongan kertas)

• Latihan soal campuran biar lebih paham konteks

• Gunakan warna buat bedain penyebut/pembilang

• Kerjakan step by step, jangan lompat langsung ke hasil

Dan yang paling penting: jangan takut salah. Pecahan itu bisa kelihatan menakutkan, tapi sebenarnya bisa jadi bagian paling menyenangkan dari matematika kalau kamu udah klik dengan polanya.

Penutup: Bukan Musuh, Tapi Teman Logika

Dulu aku pikir pecahan adalah musuh. Tapi sekarang, aku sadar bahwa pecahan itu adalah latihan logika dalam bentuk paling sederhana. Dia ngajarin kita buat membagi dengan adil, memahami proporsi, dan menghargai ketepatan.

Dan dalam dunia yang serba cepat ini, kemampuan melihat bagian dari keseluruhan adalah keterampilan penting. Baik itu buat masak, ngatur uang, atau bikin keputusan.

So, kalau kamu masih ragu atau takut sama pecahan—tenang. Ambil nafas, buka pikiran, dan coba lihat lagi: semua akan terasa lebih mudah kalau kita pelan-pelan.

Kotak-kotak unik di pecahkan dengan rumus: Himpunan: Pahami Notasi, Diagram Venn, dan Operasi Dasarnya