Waktu pertama kali saya ketemu kata trigonometri, jujur aja, saya pikir ini ilmu buat orang yang mau jadi insinyur atau ilmuwan doang. Tapi ternyata, setelah saya paham konsep dasarnya, saya baru sadar—ilmu ini kepakai banget di mana-mana. Dari arsitek, pilot, tukang bangunan, sampai desainer game, semuanya pakai trik-trik trigonometri.
Nah, artikel ini akan bahas apa itu sin, cos, tan, kenapa penting, dan gimana cara ngitungnya dengan simpel. Santai aja, kita bahas pelan-pelan, pakai bahasa yang gampang dicerna, dan tentu saja pakai contoh biar kamu nggak pusing sendiri.
Apa Itu Trigonometri?
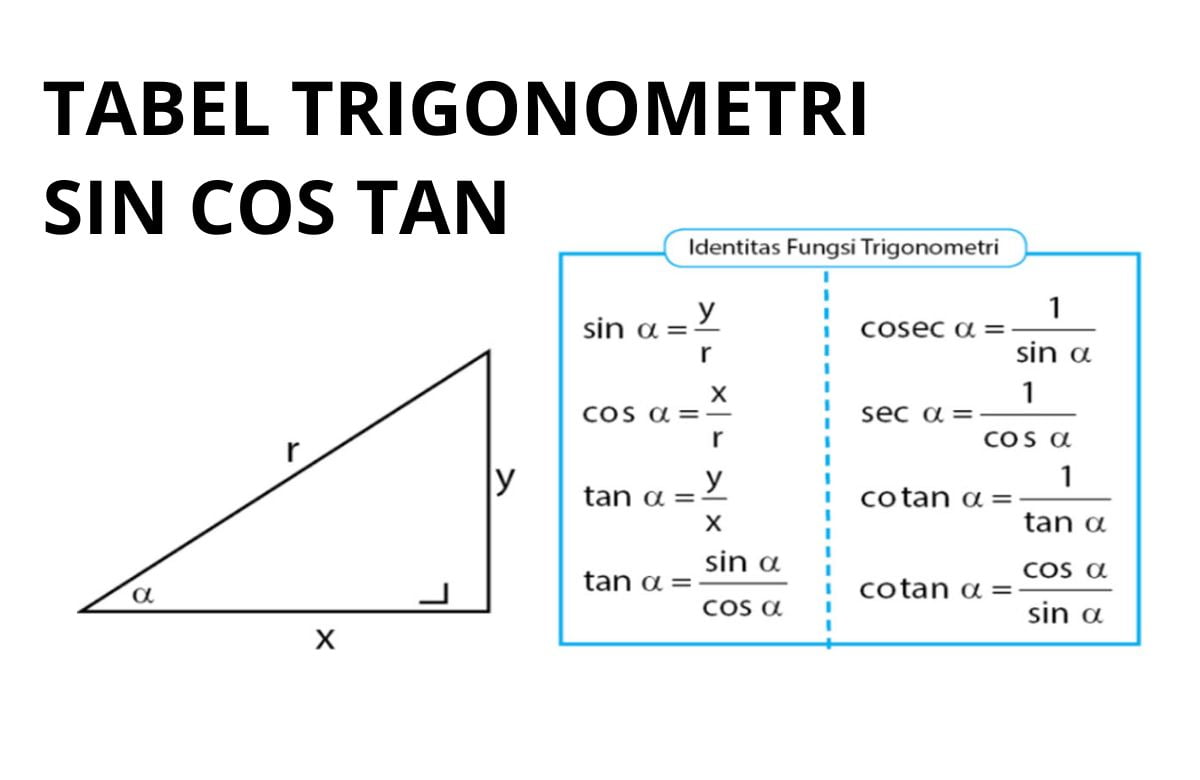
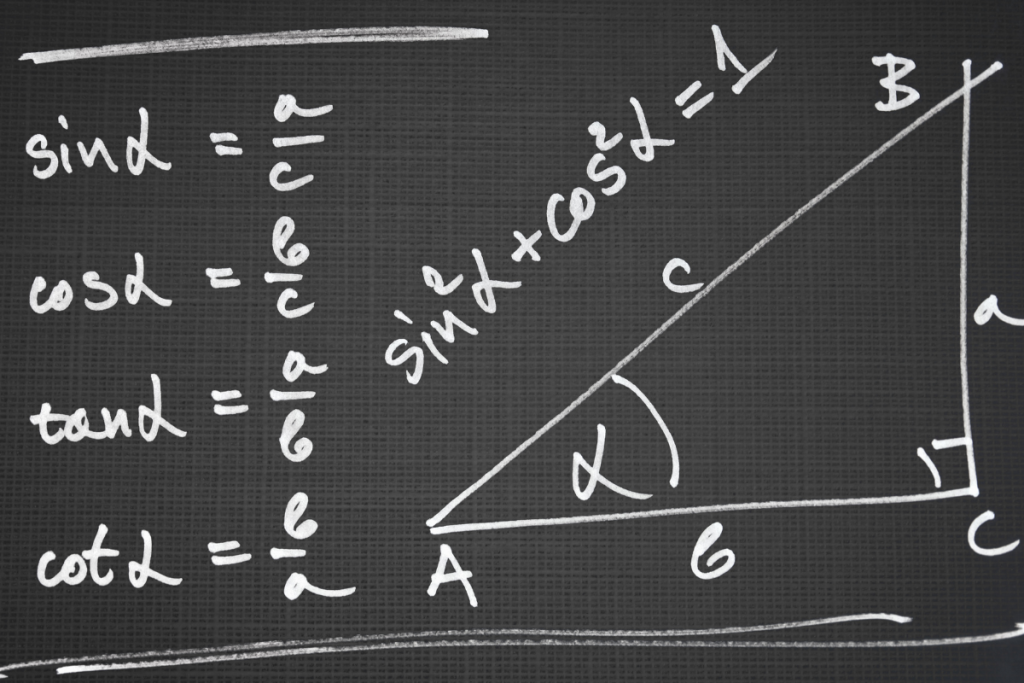
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga siku-siku. Nama “trigonometri” berasal dari bahasa Yunani, “trigonon” (tiga sudut) dan “metron” (mengukur).
Kunci utama dalam trigonometri adalah:
-
Sudut (biasanya dilambangkan sebagai θ / theta)
-
Sisi depan sudut (opposite)
-
Sisi samping sudut (adjacent)
-
Sisi miring (hipotenusa)
Nah, dari sini muncul tiga fungsi dasar pengetahuan yang jadi pondasi:
-
Sine (sin) = opposite / hypotenuse
-
Cosine (cos) = adjacent / hypotenuse
-
Tangent (tan) = opposite / adjacent
Saya suka pakai trik SOH CAH TOA buat nginget:
-
Sin = Opposite / Hypotenuse
-
Cos = Adjacent / Hypotenuse
-
Tan = Opposite / Adjacent
Penjelasan Lewat Segitiga
Bayangin kamu punya segitiga siku-siku. Satu sudutnya 90°, dan sudut lainnya kita sebut θ. Maka:
-
Sisi depan sudut θ → seberangnya
-
Sisi samping → di samping sudut θ
-
Hipotenusa → sisi terpanjang (selalu di depan sudut 90°)
Contohnya:
Kalau panjang sisi depan θ = 3 cm, sisi samping = 4 cm, dan sisi miring = 5 cm, maka:
-
sin θ = 3 / 5 = 0.6
-
cos θ = 4 / 5 = 0.8
-
tan θ = 3 / 4 = 0.75
Mudah kan?
Fungsi Trigonometri di Kehidupan Nyata
Banyak banget penggunaan trigonometri di dunia nyata. Beberapa di antaranya:
-
Menghitung tinggi pohon atau gedung dari kejauhan
-
Menentukan jarak antara dua titik di peta atau laut
-
Mendesain game dan animasi (khususnya gerakan dan sudut)
-
Dalam musik elektronik, grafik gelombang juga pakai sin dan cos
-
Membuat jembatan dan bangunan dengan akurasi tinggi
Dan kalau kamu suka drone, GPS, atau astronomi, pasti ketemu fungsi ini lagi dan lagi.
Situs seperti Khan Academy punya banyak video penjelasan trigonometri dari dasar sampai lanjutan kalau kamu pengin belajar lebih dalam dengan visualisasi interaktif yang jelas.
Cara Menghitung Tanpa Kalkulator: Sudut Istimewa
Ada beberapa sudut “istimewa” yang sering keluar di soal-soal:
| Sudut | sin | cos | tan |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | undef |
Penting buat kamu hafalin karena sering muncul di ujian. Kalau udah familiar, kamu bisa kerjain soal tanpa kalkulator sama sekali.
Hubungan antara Sin, Cos, dan Tan
Ternyata ketiga fungsi ini saling berhubungan:
-
tan θ = sin θ / cos θ
-
sin² θ + cos² θ = 1
Contoh:
Kalau sin θ = 3/5 → cos² θ = 1 – (3/5)² = 1 – 9/25 = 16/25 → cos θ = 4/5
Maka tan θ = 3/4
Logis, kan?
Grafik Fungsi Trigonometri
Kalau kamu suka visual, trigonometri juga bisa digambarkan dalam bentuk gelombang. Fungsi sin dan cos membentuk grafik seperti gelombang laut.
-
Fungsi sin dan cos: periodik (ulang terus tiap 360°)
-
Fungsi tan: grafik naik tak terbatas, dengan asimtot vertikal di titik-titik tertentu
Ini dipakai di analisis suara, getaran, dan sinyal digital.
Trigonometri dalam Koordinat Kartesius
Ketika sudut tidak hanya ada di segitiga, tapi juga pada bidang datar (x dan y), trigonometri tetap berlaku. Biasanya kita pakai lingkaran satuan (unit circle):
-
sin θ = y koordinat
-
cos θ = x koordinat
-
tan θ = y/x
Dengan sistem ini, kamu bisa dapat nilai sin, cos, tan untuk sudut lebih dari 90°, bahkan sudut negatif.
Identitas Trigonometri Lanjutan
Untuk level menengah, ada rumus-rumus lanjutan yang berguna di SMA atau kuliah:
-
sin(a ± b) = sin a cos b ± cos a sin b
-
cos(a ± b) = cos a cos b ∓ sin a sin b
-
tan(a ± b) = (tan a ± tan b) / (1 ∓ tan a tan b)
Identitas ini penting untuk menyederhanakan bentuk aljabar trigonometri.
Contoh Soal dan Pembahasannya
Soal 1
Jika sin θ = 0.6 dan θ ada di kuadran I, berapa nilai cos θ dan tan θ?
Jawaban:
cos² θ = 1 – sin² θ = 1 – 0.36 = 0.64
cos θ = √0.64 = 0.8
tan θ = 0.6 / 0.8 = 0.75
Soal 2
Hitung tinggi tiang bendera jika bayangannya 6 m dan sudut elevasinya 60°.
Jawaban:
tan 60° = √3
tan θ = tinggi / bayangan → √3 = x / 6
x = 6√3 ≈ 10.39 m
Soal-soal seperti ini sering muncul di ujian masuk universitas atau seleksi CPNS loh.
Tips Belajar Trigonometri
-
Gambar segitiga setiap kali dapat soal. Bantu banget.
-
Gunakan kalkulator scientific untuk ngecek hasil.
-
Latihan soal itu wajib. Nggak cukup paham teori.
-
Pakai warna berbeda untuk tandai sisi-sisi (bantu visualisasi).
-
Coba belajar sambil ngajarin orang lain. Itu cara tercepat buat paham.
Trigonometri dalam Dunia Nyata
Saya pernah bantu sepupu saya mengukur kemiringan atap rumahnya pakai alat sederhana. Dengan pakai sudut dan satu sisi, kita bisa hitung tinggi bagian atap yang belum dibangun. Praktis banget!
Dan di dunia teknologi, fungsi trigonometri dipakai di:
-
GPS dan pemetaan satelit
-
Motion capture di film dan game
-
Algoritma drone
-
Desain robotika
Jadi jangan anggap enteng ilmu ini. Walaupun kelihatannya rumit di awal, begitu paham, trigonometri justru jadi alat yang luar biasa serbaguna.
Kesimpulan: Sin, Cos, Tan Itu Gampang Kalau Paham Logikanya
Trigonometri mungkin terdengar menyeramkan di awal, tapi aslinya itu cuma soal hubungan antara sisi dan sudut. Kalau kamu bisa ngafalin SOH CAH TOA dan ngerti logika segitiga, sisanya tinggal latihan aja.
Jangan lupa, kamu nggak perlu hafal semua rumus langsung. Mulailah dari yang dasar. Pelan-pelan. Nanti kalau kamu udah ngerti sin cos tan itu apa, kamu bakal bisa ngitung hal-hal yang dulunya kamu pikir cuma bisa dilakukan ahli matematika.
Dan yang paling penting: jangan takut salah. Saya sendiri butuh waktu lama buat paham, dan itu normal.
Gabungkan hal kecil jadi utuh dengan: Integral dan Aplikasinya: Gabungan Kecil Jadi Besar